Series Fourieriana

Undae quadratae sunt depictae primae quattuor summae $\sum _{i=1}^{4}\left[a_{i}\cos {\frac {2\pi i}{T}}t+b_{i}\sin {\frac {2\pi i}{T}}t\right]$ seriei Fourierianae.

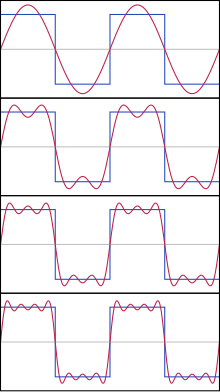
Series Fourieriana in mathematica est series ad quamvis functionem periodicam ex functionibus sinusoidalibus cosinusoidalibusque describendam vocata. Investigatio seriei Fourierianae est pars analysis Fourierianae. Vicissatim singulares functiones trigonometricas quavis ex functione periodica recuperari licet, quod transformatio Fourieriana nominatur.

Sequentia et Series

Conferatur pagina principalis: Sequentia (mathematica).

Sequentia est familia tabula cum obiectis finitis (obiectum 1, obiectum 2, obiectum 3) sive infinitis (obiectum 1, obiectum 2, obiectum 3, obiectum 4, ... etc.). Quoque obiecto $a$ ergo index $i$ proprius est, vulgo $a_{i}$. Obiecto primo indicis numerus est unum ($a_{1}$), secundo duo ($a_{2}$), etc. Exemplum series finita cum decem obiectis (86, 73, 67, 73, 80, 65, 69, 68, 73, 65) datur primo enim obiecto ($a_{1}$) valor octoginta sex est, septuaginta tres et secundo ($a_{2}$) et quarto ($a_{4}$) et nono ($a_{9}$). Infinitis invicem seriebus obiecta infinita sunt, per exemplum (3, 1, 4, 1, 5, 9, 2, 6, ...). Earum saepe primi indicis numerus 0 eligitur ($a_{0}$).

Conferatur pagina principalis: Series (mathematica).

Seriei Fourierianae cognitionis series S est summa illius non raro infinitae sequentiae cum sigma littera Graeca indicata:

• $S=a_{0}+a_{1}+a_{2}+a_{3}+\dots =\sum _{i=0}^{\infty }a_{i}$

Tamen serierum Fourierianarum obiectis non solum valores singulares sed summae ipsarum ex duobus coefficientis $a_{i}$ et $b_{i}$ cum functionibus et sinusoidali et cosinusoidali sunt: obiectum i est $a_{i}\cos +b_{i}\sin$.

Definitio seriei Fourierianae

Cum superioribus functionibus trigonometricis seriei Fourieriana (infinitae) enim haec forma est:

• $f(t)\sim {\frac {a_{0}}{2}}+\sum _{i=1}^{\infty }\left[a_{i}\cos {\frac {2\pi i}{T}}t+b_{i}\sin {\frac {2\pi i}{T}}t\right]$ cum indicibus i, $\pi$ = 3.1415926..., periodo T (functio periodica consideratur)

Nexus interni

• Euleri identitas
• Ioannes Baptista Iosephus Fourier
• Lemniscus